# 12865 평범한 배낭
https://www.acmicpc.net/problem/12865
12865번: 평범한 배낭
첫 줄에 물품의 수 N(1 ≤ N ≤ 100)과 준서가 버틸 수 있는 무게 K(1 ≤ K ≤ 100,000)가 주어진다. 두 번째 줄부터 N개의 줄에 거쳐 각 물건의 무게 W(1 ≤ W ≤ 100,000)와 해당 물건의 가치 V(0 ≤ V ≤ 1,000)
www.acmicpc.net
⭐ 코드
import sys
input = sys.stdin.readline
N, K = map(int, input().split())
bag = [(0,0)] # 인덱스 0자리 차지하기
for _ in range(N):
W, V = map(int, input().split())
bag.append((W,V))
dp = [[0] * (K+1) for _ in range(N+1)]
for i in range(1, N+1):
W, V = bag[i] # 인덱스 1부터 꺼내기
for j in range(1, K+1):
if (j - W) < 0:
dp[i][j] = dp[i-1][j]
else:
dp[i][j] = max(dp[i-1][j], dp[i-1][j-W] + V)
print(dp[N][K])📝 풀이
문제에서 N은 물품의 수, K는 버틸 수 있는 무게, W는 물품의 무게, V는 물품의 가치를 나타낸다. 문제에서의 핵심은 K를 넘지 않는 선에서 V의 최댓값을 구하면 된다.
전제 조건 자체는 어렵지 않아보였는데, 조건을 만족하는 코드를 작성하는게 어려웠다. 구글링을 해보니 1차원 배열로 푸는 방법이 있고 시간복잡도도 훨씬 낮았지만 직관적으로 와닿지 않아서 2차원 배열로 접근했다.
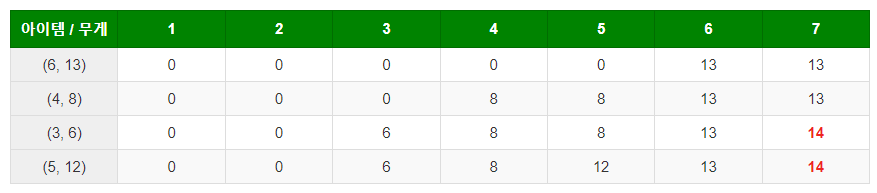
| 아이템 / 무게 | 1 | 2 | 3 | 4 | 5 | 6 | 7 |
| (6, 13) | 0 | 0 | 0 | 0 | 0 | 13 | 13 |
| (4, 8) | 0 | 0 | 0 | 8 | 8 | 13 | 13 |
| (3, 6) | 0 | 0 | 6 | 8 | 8 | 13 | 14 |
| (5, 12) | 0 | 0 | 6 | 8 | 12 | 13 | 14 |
허용 무게를 중심으로 가치의 합을 구하면 위와 같다. 문제에서는 허용 무게가 7이니까 7을 기준으로 V의 최댓값은 14이다. 3행의 (3,6) 물품을 포함하게되면 (4, 8)을 포함해도 허용범위의 무게이기 때문에 이때가 V의 최댓값이 된다.
2차원배열의 dp[i][j]의 역할은 다음과 같다
dp[i][j] = 처음부터 i번째까지의 물건을 살펴보고, 배낭의 용량이 j였을 때 배낭에 들어간 물건의 가치합의 최댓값
그렇기 때문에 N번째까지의 물건을 살펴보고 나서 용량 K의 최댓값은 dp[N][K]에 저장되게 되고 해당 값을 출력하게 되면 정답이 된다.
🔓 정답 코드 뜯어보기
import sys
input = sys.stdin.readline
# N은 물품의 수
# K는 버틸 수 있는 무게
# W는 각 물품의 무게
# V는 물품의 가치
N, K = map(int, input().split())
bag = [(0,0)] # 인덱스 0자리 차지하기
for _ in range(N):
W, V = map(int, input().split())
bag.append((W,V))
dp = [[0] * (K+1) for _ in range(N+1)]먼저 input값을 다 받아주고 bag 리스트를 생성해준다. 인덱스 0자리를 차지하기 위해 [(0,0)]를 초기값으로 설정해준다. dp리스트 또한 무게(k)와 물품의 수(N)보다 한개 많게 범위를 설정해서 생성해준다.
for i in range(1, N+1): # 1번
W, V = bag[i] # 인덱스 1부터 꺼내기
for j in range(1, K+1): # 2번
if (j - W) < 0: # 3번
dp[i][j] = dp[i-1][j]
else: # 4번
dp[i][j] = max(dp[i-1][j], dp[i-1][j-W] + V)
print(dp[N][K]) # 5번# 1번
인덱스 설정을 0부터 했으므로 range는 (1,N+1)까지 설정해준다. bag에 저장한 인덱스를 W,V에 할당해준다.
# 2번
똑같이 무게보다 1크게 범위를 설정해주고 반복문을 실행시켜준다.
# 3번
j(무게) - w(물품의무게)가 < 0보다 작으면 아래 로직을 실행시켜준다.
dp[i][j] = dp[i-1][j]
위 로직은 i번째 아이템을 챙기지 않았을 때의 최댓값이다.
# 4번
위의 로직에 해당하지 않는다면
챙기지 않았을 때 (dp[i-1][j]) 와 i번째 아이템을 챙겼을 때 갖는 최댓값 dp[i-1][j-w] + v을 비교해서 큰 값을 저장시켜준다.
# 5번
그림에서와 같이 dp[n][k]를 해주면 최댓값이 출력된다.
'Algorithm' 카테고리의 다른 글
| [python] 백준 7569번: 토마토(BFS) (0) | 2023.02.23 |
|---|---|
| [python] 백준 2293번: 동전1(DP) (0) | 2023.02.18 |
| [python] 백준 12904번: A와 B(Greedy) (2) | 2023.02.16 |
| [python] 백준 11501번: 주식(Greedy) (0) | 2023.02.16 |
| [python] 백준 16236번: 아기 상어(BFS) (0) | 2023.02.15 |